The erlang is a unit of traffic density in a telecommunications system. One erlang is the equivalent of one call (including call attempts and holding time) in a specific channel for 3600 seconds in an hour. The 3600 seconds need not be, and generally are not, in a contiguous block.
In digital telecommunications, the voice signals are compressed. This makes it possible for one channel to carry numerous calls simultaneously by means of multiplexing. In theory, there are many ways in which a channel can carry a certain number of erlangs. For example, a traffic density of 3 erlangs can consist of three simultaneous calls, each lasting for an hour (a total of 10,800 seconds); it can consist of six calls, each of which are allocated 30 minutes (1800 seconds) of time during the hour; it might consist of 180 calls, each of which occupy one minute (60 seconds) of time during an hour.
Smaller units of traffic density are sometimes used. The hundred or centum call second or CCS is the equivalent of one call for 100 seconds out of an hour. A traffic density of 1 CCS is equal to 1/36 erlang. An erlang can be applied to the group of lines in a telephone trunk line or to the traffic in a telephone call center.
The term is named after the Danish telephone engineer, A. K. Erlang, the originator of queueing theory.
So this week, I was assigned to do research on ERLANG. There are many types of Erlang, however, I was asked to to find more details on Eralng A, Erlang C and also Erlang B. Other than that, I was also asked to find the spreadsheet for these Erlangs and their respective formula in telecommunication field.
Palm introduced a simple (tractable) way to model abandonment. He suggested enriching Erlang-C (M/M/n) in the following manner. Associated with each arriving caller there is an exponentially distributed patience time with mean a-1. An arriving customer encounters an offered waiting time, which is defined as the time that this customer would have to wait given that her or his patience is infinite. If the offered wait exceeds the customer’s patience time, the call is then abandoned, otherwise the customer awaits service. The patience parameter a will be referred to as the individual abandonment rate.
In call centers, Erlang-A is used, or should be used, to support solutions of the staffing problem, namely: how many agents should be answering calls during a specified time period. Typically, the goal is to provide a satisfactory service level (for example, fraction abandoning less than 3%), but sometimes one optimizes an economic measure - minimize cost or maximize revenues.
There are certain parameters that are important in Erlang A :
1. Arrival : Arrivals of incoming calls are typically assumed Poisson, with time-varying arrival rates. The goal is to estimate/predict these arrival rates, over short time-intervals (15, 30 minutes or one hour), chosen so that the rates are approximately constant during an interval. Then the time-homogeneous model is applied separately over each such interval.
2. Service : Service durations are assumed exponential. Average service times tend to be relatively stable from day to day. In practice, service consists of several phases, mainly talk time, wrap-up time (after-call work), and what is sometimes referred to as auxiliary time. An easier-to-grasp notion is thus “idle-time”, namely the time that an agent is immediately accessible for service.
3. Number of Agents
4. Patience
ERLANG C
Erlang C is a traffic modeling formula used in call center scheduling to calculate delays or predict waiting times for callers. Erlang C bases its formula on three factors: the number of reps providing service; the number of callers waiting; and the average amount of time it takes to serve each caller. Erlang C can also calculate the resources that will be needed to keep wait times within the call center's target limits. This method assumes that there are no lost calls or busy signals, and therefore may overestimate the staff that is required.
Figure : Erlang C Traffic System
Clearly some of the assumptions of the Erlang C model are not true for a call center. For example, there are only a finite number of trunks, hence only a finite number of places where calls can be parked while waiting for service. But, if the number of trunks is quite large, then as a practical matter, there may be no situation when all trunks are busy, hence the assumption of infinitely many waiting positions might "almost" be true. Similarly, the assumptions of Poisson arrivals and exponential service times will not hold exactly. Nevertheless, experience over many decades has shown that using the Erlang C model can give helpful insights into the operation of agent groups in call centers, provided that
(1) there are a large number of trunks (hence many waiting slots),
(2) the assumptions of Poisson arrivals and exponential service times are approximately correct over the period being studied,
(3) waiting calls are handled first-come-first-served.
Figure : Calculation formula for Erlang C
Figure : Spreadsheet for Erlang C
ERLANG B
Erlang B is a modeling formula that is widely used in call center scheduling. The formula can be used to calculate any one of the following three factors if you know or predict the other two:
• Busy Hour Traffic (BHT): the number of hours of call traffic during the busiest hour of operation
• Blocking: the percentage of calls that are blocked because not enough lines are available
• Lines: the number of lines in a trunk group.
Erlang B can determine the number of trunks, or lines, needed to handle a calling load during a one-hour period. However, the formula assumes that lost calls are cleared; i.e., if callers get a busy signal, they will never retry. This assumption means that Erlang B can underestimate the number of trunks needed. For this reason, it is best used in situations with few busy signals. The Erlang B Extended formula takes into account the callers who will immediately retry if their calls do not go through.
Figure : Erlang B Traffic System
Generations of telephone engineers have successfully used the Erlang B model to predict blockage in telephone trunk groups, despite the fact that no telephone trunk group exactly matches the assumptions of Erlang B. Perhaps the most questionable assumption is that when a caller is blocked (i.e., finds all trunks busy), the customer then goes away, never to return. If there is a lot of blocked, customers start a cycle of re-calling in order try to get through, then the assumption of Poisson arrivals will fail. (Agner Erlang himself dealt with re-calling by using the Erlang C model. He imagined that re-calling customers were placing themselves in a virtual waiting queue.)
Figure : Calculation Formula for Erlang B
Figure : Spreadsheet of Erlang B





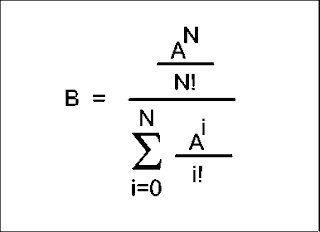

No comments:
Post a Comment